At the end of this blog we should be able to solve this problem:
Imagine you are working at a data analytics firm where you need to repeatedly multiply a massive square matrix (of order n) by a single vector to update certain predictive models. Because the matrix is so large, you decide to distribute it among multiple parallel processes using MPI, employing a block-column distribution strategy. Specifically, Process 0 reads the entire matrix file and sends different blocks of columns to the other processes. Each process, in turn, multiplies its own block of columns by the vector. The final step is to combine all partial products to form the resulting output vector, for which MPI Reduce scatter can prove especially valuable. Your task is to describe how you would implement this block-column distribution and matrix-vector multiplication in MPI (initializing MPI, distributing data, performing local multiplications, reducing the results, and finalizing). As part of this description, outline the necessary MPI function calls and illustrate the workflow with concise code.
Understanding vector multiplication
Before diving into the specifics of our problem, it’s important to lay a solid foundation. We first need to understand what vector multiplication is and how it works mathematically. A clear grasp of the fundamentals will make the implementation much easier. After exploring different resources, I came across this site, which explains vector multiplication in a straightforward and intuitive way. If you’re new to the concept, I highly recommend going through it to build a strong understanding before moving forward.
However, to further simplify things, the following is a example of a square vector and a single vector:
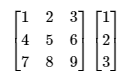
And the above simply bowls down to the following while carrying out the multiplication:

If you understand the above then you are good to proceed.
Implementing vector multiplication in C
Now, once you have understood vector multiplication, you need to understand how a vector is represented in C. In C, vectors are represented using arrays, a data structure you must be familiar with. If you are not, please refer to any basic C language book, and you should be good to go.
For simplicity, we will consider static arrays, which do not grow or change over time. Once we declare an array with a fixed number of elements, those values remain throughout the program. This is a reasonable assumption for most cases where the size of the vector is known in advance.
Single vector representation in C
A single vector in C is represented as a one-dimensional array, where each element is accessed using an index. The following is a sample single vector representation in C language:
int vector[5] = {1, 2, 3, 4, 5}; // A vector with 5 elementsSquare Vector Representation in C
A square vector in C is typically represented as a two-dimensional array, where the number of rows equals the number of columns (i.e., an N × N matrix).
The following is a fixed-size (3×3) square vector representation in C:
int square_vector[3][3] = {
{1, 2, 3},
{4, 5, 6},
{7, 8, 9}
};Here, square_vector[i][j] refers to the element at the i-th row and j-th column.
Simple Vector Multiplication in C
Now, let’s start by understanding how simple vector multiplication is implemented in C. Below is a sample code snippet that provides a clear visualization of the process:
vector_multiplication_simple.c
#include <stdio.h>
#define N 3 // Size of the square vector and single vector
void multiplyVector(int square_vector[N][N], int single_vector[N], int result[N])
{
printf("Square Vector and Single Vector Multiplication Process:\n");
for (int i = 0; i < N; i++)
{
result[i] = 0;
printf("\nComputing result[%d] (Row %d of square vector * single vector):\n", i, i);
for (int j = 0; j < N; j++)
{
printf(" Multiplying square_vector[%d][%d] (value: %d) with single_vector[%d] (value: %d) -> %d * %d = %d\n",
i, j, square_vector[i][j], j, single_vector[j],
square_vector[i][j], single_vector[j],
square_vector[i][j] * single_vector[j]);
result[i] += square_vector[i][j] * single_vector[j];
}
printf(" Sum of row %d = %d (Stored in result[%d])\n", i, result[i], i);
}
}
int main()
{
int square_vector[N][N] =
{
{10, 20, 30},
{40, 50, 60},
{70, 80, 90}
};
int single_vector[N] = {5, 6, 7}; // Single vector
int result[N]; // Resultant vector
multiplyVector(square_vector, single_vector, result);
// Print the final result
printf("\nFinal Resultant Vector:\n");
for (int i = 0; i < N; i++)
{
printf("result[%d] = %d\n", i, result[i]);
}
return 0;
}Now that we have the code, let’s walk through it step by step to understand how it works. The goal of this program is to multiply a square vector. This is a 3×3 matrix. It is multiplied with a single vector, which is a 1D array. The result is stored in another vector. Understanding how these vectors are represented in C and how the multiplication takes place is key to following this implementation.
Representation of the Square Vector and Single Vector
In this program, a square vector is simply a two-dimensional array. Each row represents a set of coefficients. These coefficients will interact with the single vector. This matrix remains fixed in size (3×3) for simplicity. The single vector is a one-dimensional array containing three elements. During multiplication, each row of the square vector multiplies with the single vector. This process produces a new one-dimensional result vector.
The square vector is represented as:
int square_vector[N][N] =
{
{10, 20, 30},
{40, 50, 60},
{70, 80, 90}
};Each row of this matrix will be multiplied with the single vector:
int single_vector[N] = {5, 6, 7}; The result of this multiplication will be stored in the result vector:
int result[N]; This result vector starts as an empty array and gets populated as the program performs the multiplication.
Understanding the Multiplication Process
The multiplication follows a simple row-wise computation. Each row of the square vector is multiplied element-wise with the corresponding elements of the single vector. The sum of these products gives the value for that row in the result vector.
For instance, when multiplying the first row of square_vector with single_vector, the computation is as follows:
// Computing result[0]
result[0] = (10 * 5) + (20 * 6) + (30 * 7) = 50 + 120 + 210 = 380Similarly, for the second row:
// Computing result[1]
result[1] = (40 * 5) + (50 * 6) + (60 * 7) = 200 + 300 + 420 = 920;And for the third row:
// Computing result[2]
result[2] = (70 * 5) + (80 * 6) + (90 * 7) = 350 + 480 + 630 = 1460;Thus, the final result vector will be:
result = {380, 920, 1460}Now lets compile the program and try to run it in the next sections.
Compiling and running the program
To compile and run the program, follow these commands:
# Compile the program
gcc vector_multiplication_simple.c -o vector_multiplication_simple
# Run the compiled executable
./vector_multiplication_simpleOnce you run the above program, you will see the output on the console.
Sample output
./vector_multiplication_simple
Square Vector and Single Vector Multiplication Process:
Computing result[0] (Row 0 of square vector * single vector):
Multiplying square_vector[0][0] (value: 10) with single_vector[0] (value: 5) -> 10 * 5 = 50
Multiplying square_vector[0][1] (value: 20) with single_vector[1] (value: 6) -> 20 * 6 = 120
Multiplying square_vector[0][2] (value: 30) with single_vector[2] (value: 7) -> 30 * 7 = 210
Sum of row 0 = 380 (Stored in result[0])
Computing result[1] (Row 1 of square vector * single vector):
Multiplying square_vector[1][0] (value: 40) with single_vector[0] (value: 5) -> 40 * 5 = 200
Multiplying square_vector[1][1] (value: 50) with single_vector[1] (value: 6) -> 50 * 6 = 300
Multiplying square_vector[1][2] (value: 60) with single_vector[2] (value: 7) -> 60 * 7 = 420
Sum of row 1 = 920 (Stored in result[1])
Computing result[2] (Row 2 of square vector * single vector):
Multiplying square_vector[2][0] (value: 70) with single_vector[0] (value: 5) -> 70 * 5 = 350
Multiplying square_vector[2][1] (value: 80) with single_vector[1] (value: 6) -> 80 * 6 = 480
Multiplying square_vector[2][2] (value: 90) with single_vector[2] (value: 7) -> 90 * 7 = 630
Sum of row 2 = 1460 (Stored in result[2])
Final Resultant Vector:
result[0] = 380
result[1] = 920
result[2] = 1460The output of the program should be pretty intuitive and self-explanatory. It clearly explains each step of the multiplication process. It shows how each element of the square vector is multiplied by the corresponding element of the single vector. Then, it follows with the summation for each row.
To summarize, the program:
- Iterates through each row of the square vector.
- Multiplies each element of the row with the corresponding element in the single vector.
- Adds up these products to compute the final value for that row in the resultant vector.
- Repeats this for all rows and prints the final computed result vector.
You have now understood how vector multiplication works in C. We are ready to take the next step. This involves solving the problem using MPI. This will allow us to distribute the computation across multiple processes, leveraging parallelism to improve efficiency.
In the next post, we will explore how to implement this using MPI. We will go step by step. This ensures that we build on what we have learned so far. Stay tuned!

Leave a Reply